In Praise of Tanh

Brothers, Sisters, Cat People and Dog People, Non-human humans and others, I write here today in praise of tanh (pronounced “tanch” like “ranch” — IYKYK.) If you regularly employ tanh to solve your computer music problems, great! If you are “what is tanh?” then read on!

Problems

You’ve got problems. I’ve got problems. We’ve all got problems. But what you don’t know yet is how many of your problems can be solved with tanh. (Probably two.) Tanh isn’t just a hyperbolic tangent! It’s a way of life, an elegant solution to a serious problem, the sonic enrichment your soggy timbres have been lacking.

Problems with amplitudes over one? No more!

Suffering from timbrel boredom? Banished!

Tanh Proper

Tanh is a function built into everything — you can find it everywhere, including your favorite audio programming language and mine, SuperCollider. It’s easy to miss though — it’s a unary operator that suffers from lack of exposure, its glam obscured by a whole host of lesser unary ops that have better social media people. You might not even be aware it exists. After all, how many hours have you spent scouring the SimpleNumber help file? Not a single one? Fear not.

Application 1: I can’t control my amplitudes!

So what is so amazing about tanh? Here’s one. You have an audio stream with amplitudes that *usually* stay below one, but occasionally exceed it. Perish the thought! What is a girl to do?

1. Manually find those spots and make tedious adjustments to your algorithms to preclude them, possibly resulting in choppy and unnatural edits to say nothing of the time lost making them.
2. Throw a compressor on it, possibly resulting in reduced dynamic range and spectral interest. Ugh.
3. Give up. You never really got this whole digital audio thing anyway. Maybe crocheting really is for you…

No! “Just throw a tanh on it!” as the old North Philly computer audio guy saying goes.*

Application 2: my sounds are boring and distortion is so expensive and hard to understand!

Your sounds are flat, they lack life, richness, and vitality. “Throw a tanh on it!” and watch your spectrum explode with vibrancy! “But, how?” you ask?

How Tanh Works

Math is complicated and as soon as we start talking about exponents, numerators, denominators, and the relationship of cosh and sinh we are going to lose folks. Suffice it to say, tanh is brilliant at solving our above two problems in one simple way — it limits input values to -1 to 1 no matter how far they exceed that range. Where input values are extreme (±3) the output values become increasingly “saturated” — closer and closer to 1, but never quite getting there. Where the high-amplitude input is sinusoidal, the output is increasingly square. The result is the accumulation of odd harmonics.

At values close to, but greater than 1, output values from tanh are less than 1. For values significantly greater than 1, the output values approach 1, but never quite get there. This means that tanh can function both as a soft limiter and as a distortion function depending on the input value. Let’s have a look.

Tanh in Color

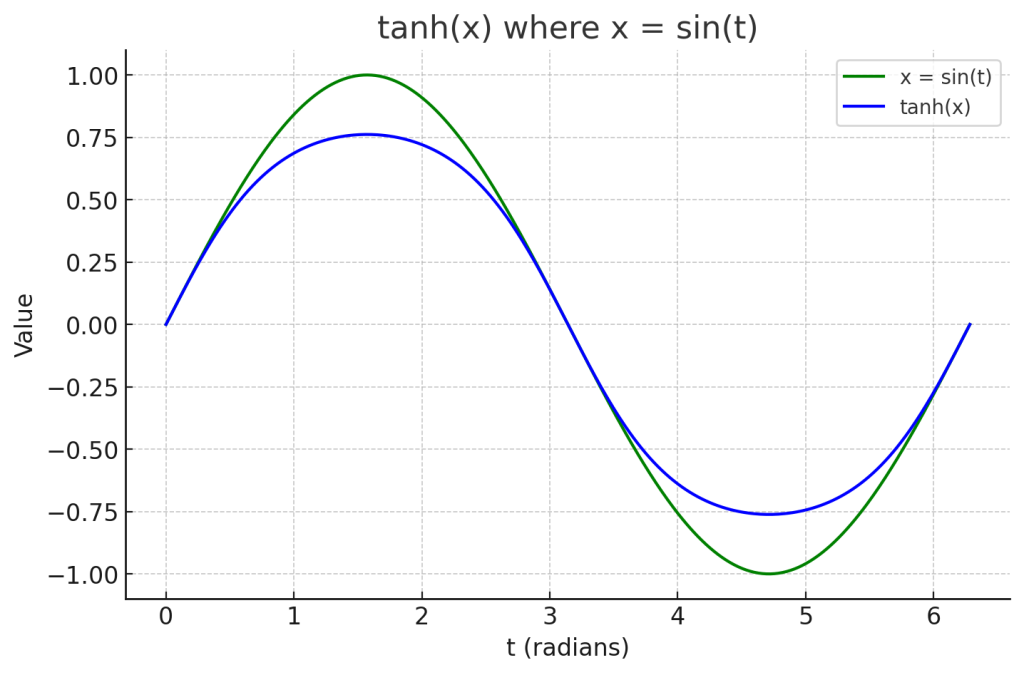
Here’s the plot with x (green curve) defined as one full sine cycle with an amplitude of 1. The blue curve shows tanh⁡(x). Since sin⁡(t) already ranges only between −1 and 1, the tanh function compresses it slightly — the output stays close to the sine shape but is “pulled in” toward the horizontal axis, because tanh is less steep inside [−1,1].

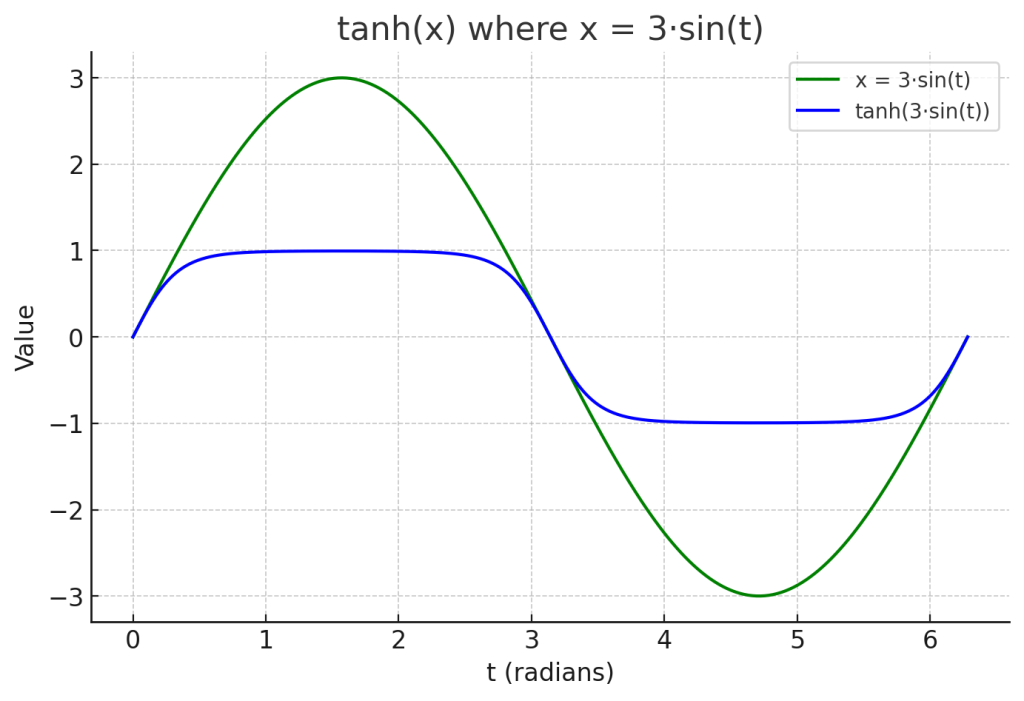
Here’s a plot with x=3*sin⁡(t) (green). The blue curve shows tanh⁡(x). Because the sine input now ranges from −3 to +3, much of it lies in the region where tanh⁡(x) has already saturated. The result is that the output (blue) gets squashed very close to −1 and +1, making it look almost like a clipped sine wave.

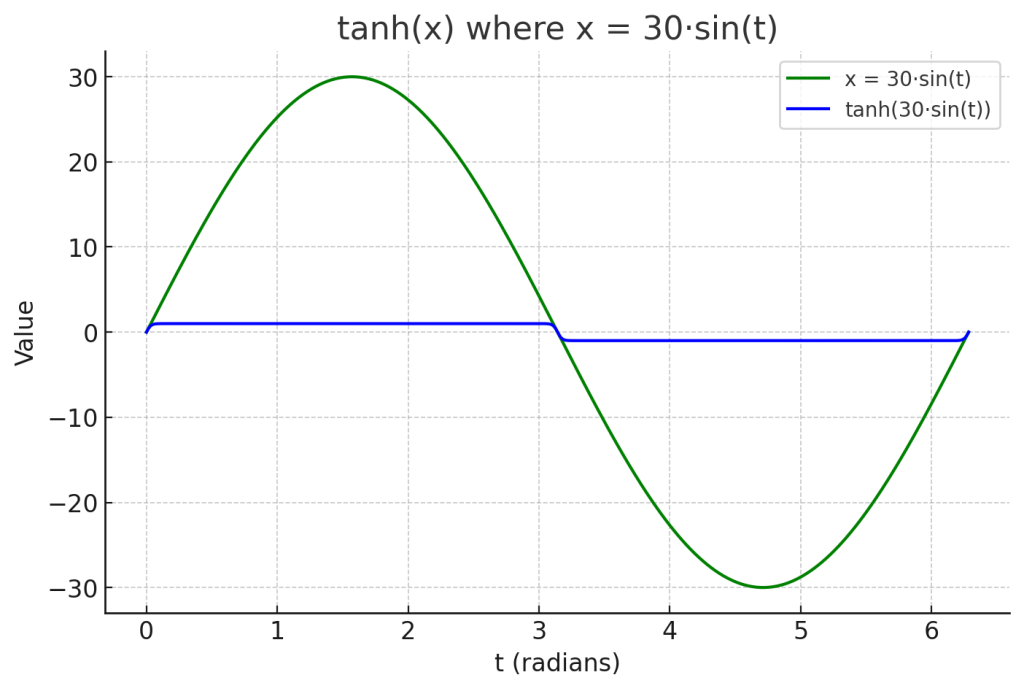
Here’s the plot with x=30*sin⁡(t). Here, the tanh(x) curve is almost indistinguishable from a square wave: it jumps between −1 and +1 and only transitions briefly near the zero-crossings of the sine input. This is difficult to see because of the range disparity between input and output. Below, the waveform comparison is clearer.

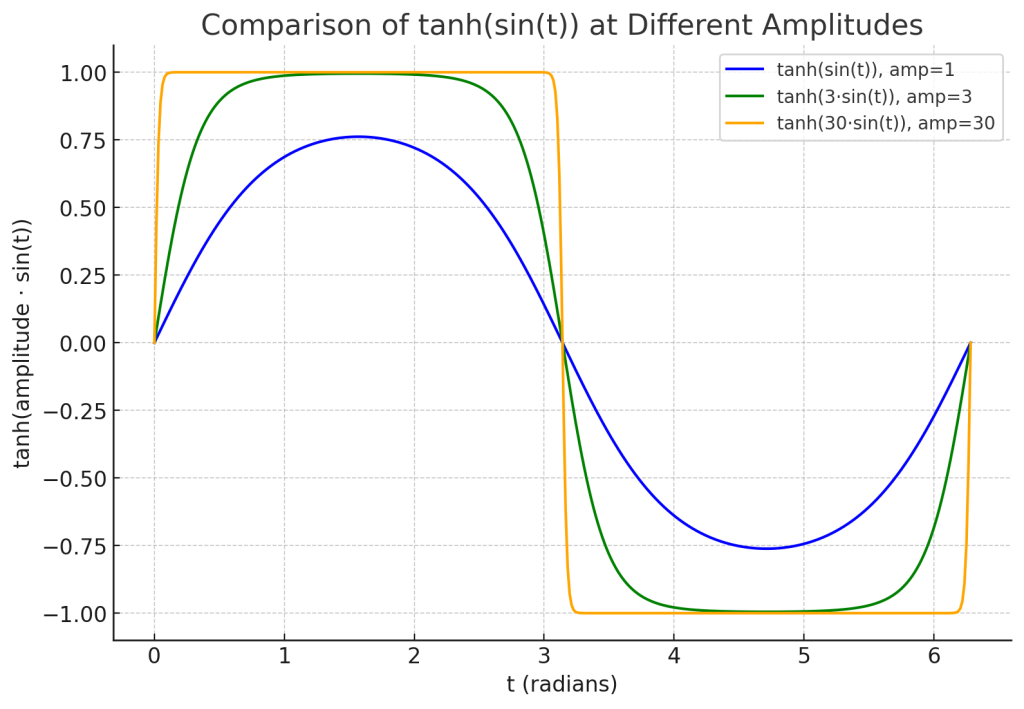
Here’s a comparison plot of the tanh(x) for amplitudes of 1 (blue), 3 (green), and 30 (orange).

• Amplitude = 1 → output is smooth, close to the sine shape.
• Amplitude = 3 → output starts flattening near ±1, creating a “soft-clipped” waveform.
• Amplitude = 30 → output is almost a perfect square wave, locked at −1 and +1 except near zero crossings.

It’s easy to see how our “I’ve got amplitudes over 1” problem is solved by tanh, but what’s not explicit in the above graphs is the harmonic effect tanh has on the input where the amplitude is significantly over 1.

Give me those harmonics!

Below are the spectral graphs of an input sinusoid (see above) with amplitudes of 3 and 30 respectively.

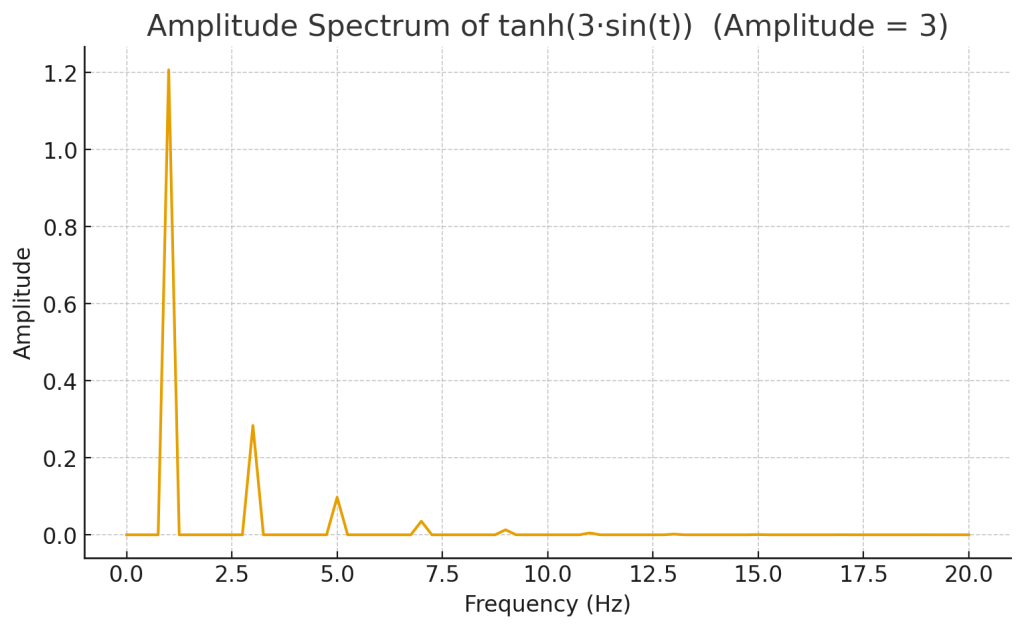
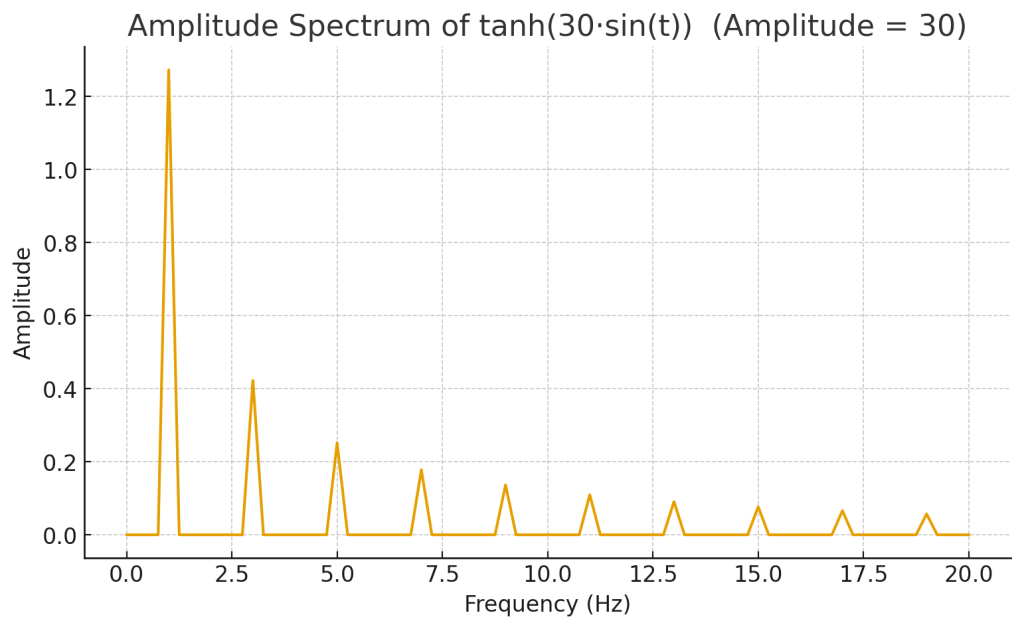
Notice that the sinusoidal signal is no longer a sinusoid (a single frequency.) At amplitude = 3, we see odd harmonics (3rd, 5th, 7th, …) appear as the nonlinearity of tanh takes effect. With an amplitude of 30 we see a clear odd-harmonic series with slowly decaying amplitudes approaching the spectrum of a square wave.

Sure sure, but what does it sound like?

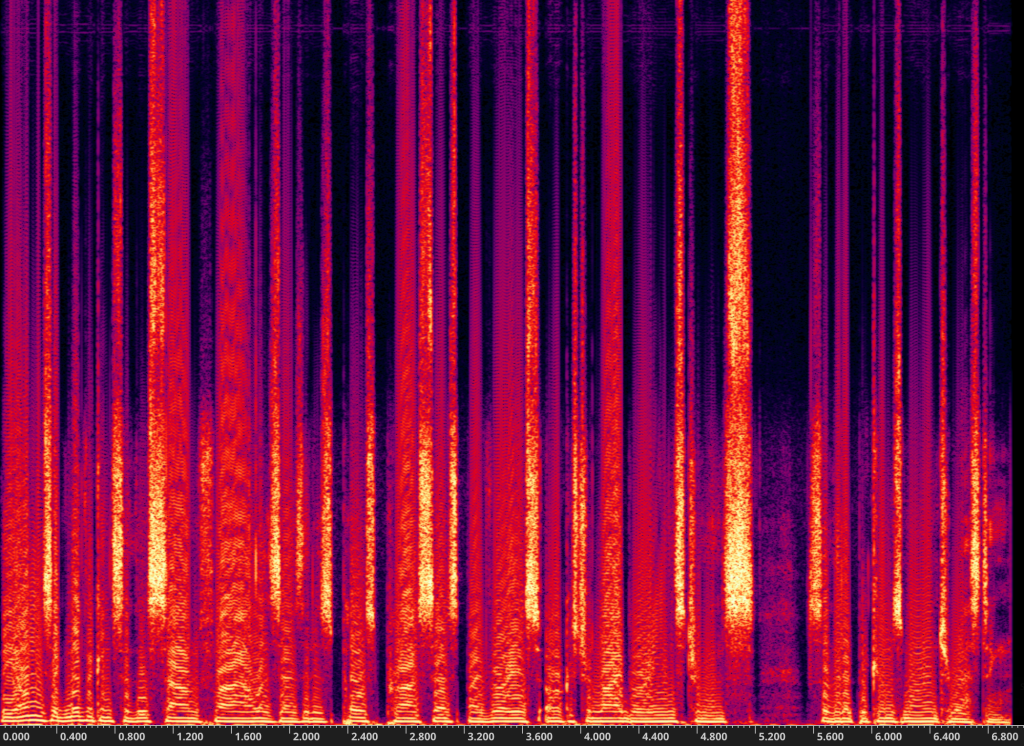
Here are three recordings of a short section of spoken word audio (Voice Test!) The first has an amplitude of 1. The second has an amplitude of 3. The third, an amplitude of 30. Above each audio clip is the spectrogram for that file.

Audio 1: Amplitude = 1

Audio 2: Amplitude = 3

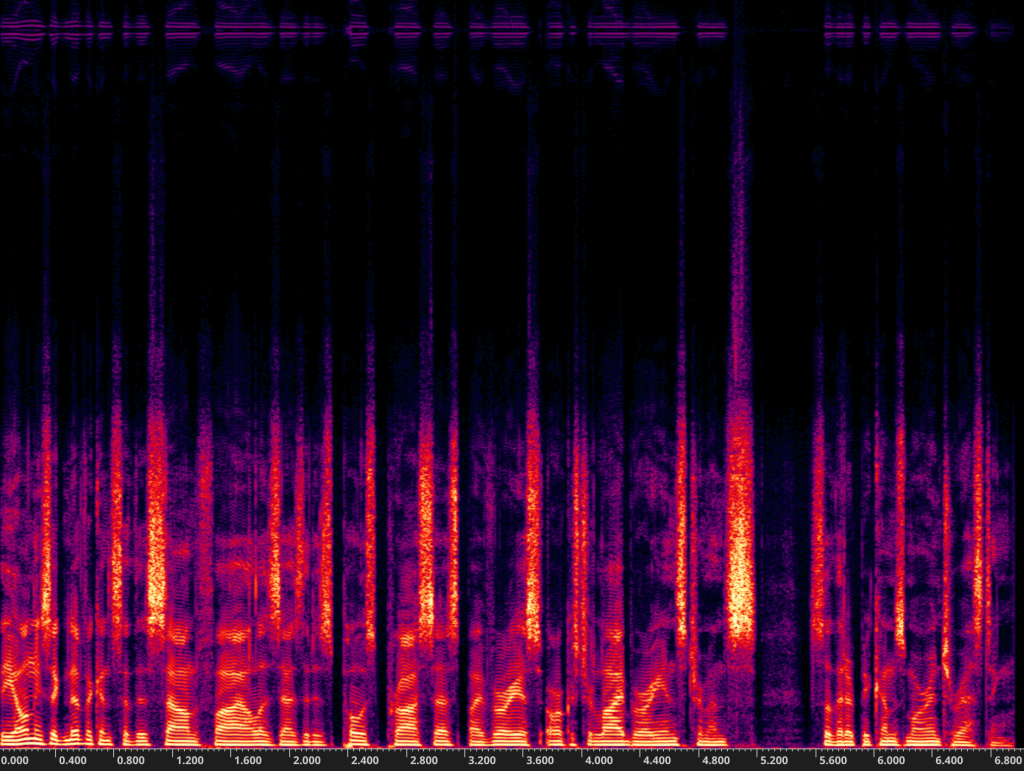
Audio 3: Amplitude = 30

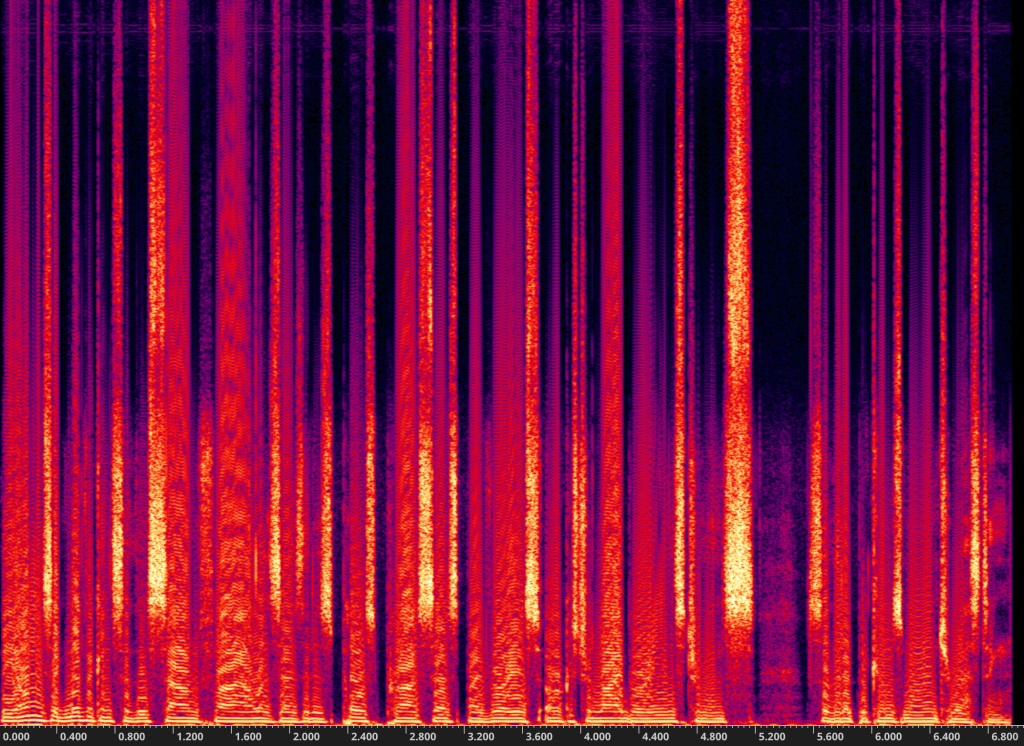
Yes yes, but this magic must be costly and difficult to use!

No, comrades! It’s as easy as this: sprinkle a little .tanh wherever your sound recipe requires it! Yes, it’s that easy! ArbitraryUgen.ar(args).tanh. Or, an example that actually works:

play { SinOsc.ar(400, 0, 30).tanh };

The above tanh turns a sinusoidal signal (SinOsc) into one closer akin the square wave (Pulse). For use as a gentle (or not) limiter, just put .tanh wherever you need to preclude values over 1. Usually this is on the output, but you may require it earlier in the signal chain if you are running processes that blow up with values greater than 1.

Tanh provides tons of utility and color opportunities. Try it today and let your friends know too!

*I probably said this at least once when I lived in North Philly decades ago. If I didn’t, I should have. (At worst this is a missed opportunity, not a lie!)